Astrophotography and Eyepiece Calculators

These spreadsheets can be used to calculate numerous useful parameters for astrophotographers and help visual astronomers to organize their eyepiece collection

Download:

Eyepiece Collection Calculator Features

  • An editable list of eyepieces which calculates power, FOV, exit pupil, etc.
  • Warnings if the resulting power is too low or too high.
  • Graphs which show the powers and the FOVs of the collection.
  • Recommended list of eyepieces focal lengths.

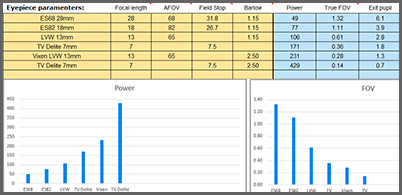
Eyepiece collection calculator screenshot

Astrophotography and CCD Calculator Features

  • Basic parameters such as FOV, resolution, airy disk, image scale, etc.
  • Planetary section with sampling rate, required barlow, video times for planets.
  • Deep Sky section with sampling rate based on seeing, required barlow, etc.
  • Vignetting and field of view, coma, focal depth, thermal shift of focus.
  • Parameters for artificial star distance, roddier test, eyepiece projection.
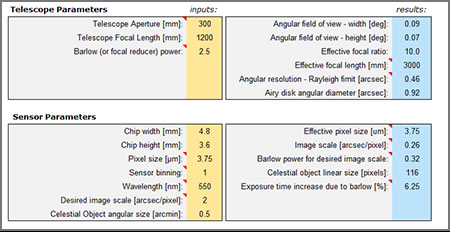
Telescope Eyepieces Calculator
Astrophotography and CCD calculator screenshot

In order to help a bit with some terminology - the following diagram provides a brief illustration of light path inside the telescope with some of its basic elements - one with an eyepiece and one with a CCD camera. The green rays are from a distant, point like source (such as a star), as it's collected by the whole aperture and focused into a single point on our retina or a CCD chip. The blue rays illustrate the maximum field of view of the telescope, usually limited by an eyepiece field stop diameter (its front lens) or a CCD chip dimensions.


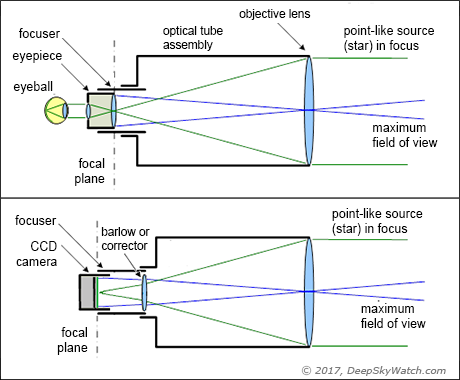
Light path inside a telescope with an eyepiece and a CCD camera

Previous Version

There is an older version of the telescope calculator, which features some additional features like formulae lists, telescope comparison, tables and graphs of magnifications and object brightness analyzis. It can be downloaded here:

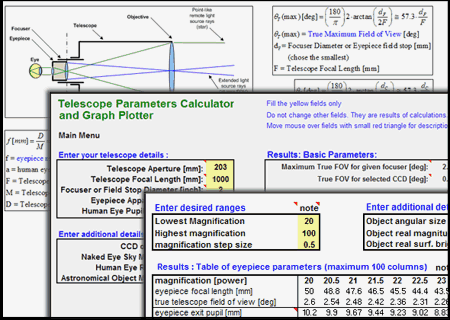
Telescope Calculator
Previous telescope calculator screenshot

Note About Surface Brightness

One of the purposes of this calculator is to bring attention to a topic often unfamiliar to amateur astronomers: The fact that apparent surface brightness (intensity per area of our retina as we see it) of an extended deep sky object is constant - it never actually increases, no matter which telescope we use.

Assume we observe the Andromeda galaxy with our naked eyes. There is a certain amount of light density (per square metre) reaching our eye's retina. Irradiance if we use radiometric therminology, or as we may simply call it, apparent surface brightness.
If we take a telescope and use magnification which gives us brightest possible image (exit pupil equals to dark adapted eye's pupil of 6-7mm) there will be no change in apparent surface brightness of the object compared to unaided eye. A mathematical proof to this is included in attached Excel file, though it can simply be backed by "Radiance Conservation Law" or "Extent Conservation Law" which is derived from the conservation of energy law.
It should be realized though that there are other factors which affect our perception of the object brightness: Contrast does increase with magnification (due to a lower background), object size also increases, so is the overall apparent magnitude.

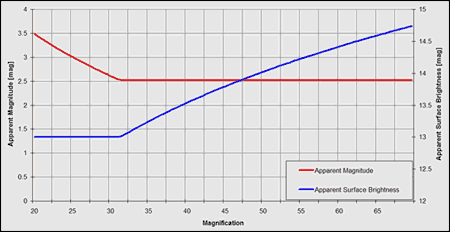
magnitude and surface brightness graph
Apparent magnitude vs apparent surface brightness

This is illustrated in the attached graph: The red chart represents apparent magnitude, and the blue one represents apparent surface brightness. Chart plotted as a function of magnification.

The breaking point on the chart shows magnification at which telescope's exit pupil equals to human eye pupil (6-7 mm). Under this magnification we begin to lose light, even though the apparent surface brightness does not change. Higher than this magnification - we start losing the apparent surface brightness, but overall magnitude will remain constant.

Bottom line: If we want to use a really low magnification (lower than our pupil allows us) - we can do it, if the goal is to fit object into field of view. But in this case observer's pupil will clip the effective aperture and some light will be lost. Though it still will be brightest possible image at given magnification with any instrument.